どうしたら我が子に数学・算数を得意になってもらうか？

数学（算数）が得意になる子の特徴

数学（算数）を勉強している生徒は、誰もが「数学ができるようになりたい」と思い、「難関中学、難関高校、難関大学の入試に通用する数学力（算数力）をつけたい」と考えているでしょう。ここでは、数学（算数）の学力向上の秘訣と、どういうタイプの生徒が「数学（算数）が得意になる生徒」なのか考えてみましょう。

数学（算数）を得意になる秘訣には、大きく三つのポイントがあります。

01　徹底的に繰り返し練習すること

数学（算数）は、スポーツを上手になるのと非常に似ています。ただし、スポーツというと大谷やイチローのように、生まれながらのセンスというか、どうしても努力だけでは補いきれない面も思い浮かんでしまうので、もっと分かりやすいものに喩えれば、筋トレのようなものと言った方が良いでしょう。

なかやまきんに君の台詞で有名になりましたが、もともとは、近畿大学准教授の谷本道哉（東大出身のスポーツ科学の第一人者）の「筋肉は裏切らない」という言葉がありますが、これは「正しい筋トレを行えば、必ず筋肉はつく」し、筋肉は「鍛えれば鍛えるだけ筋力も自信もつくから、小さい事でクヨクヨしていないで、君も筋トレして強くなろうぜ！」というメッセージとして理解されています。

要するに、筋トレと同じように、数学（算数）の勉強は繰り返し行えば行うほど力が増し、繰り返しによって培われた数学（算数）力は決して裏切りません。そして、その努力の結果は、それは別に元々数学（算数）が得意だとか、特別なセンスが必要というわけではありません。

特別なセンスや素質が必要がないという例を考えるとすると、NHKの「みんなで筋肉体操」で再ブレイクした武田真治のような芸能人を思い浮かべてみてもよいかもしれませんが、武田真治は元々別に厳つい体格をしていたわけでもなければ筋肉質というほどの体でもありませんでした。武田真治の格好良さやサックスの才能は天性のものでしょうが、彼の肉体美については、紛れもなく努力の結晶です。今のお子さんは昔の武田真治を知らないかもしれませんが、写真で見るとこれくらい違います。

武田真治《武蔵境駅徒歩30秒》武蔵野個別指導塾

まあ、昔も意外と締まった体をしているのですが、昔の武田真治は「フェミ男」と呼ばれる芸能人の代表格で、今流行のLGBTQ（＋IA）の先駈けのような人で、「ジェンダーレス男子」として、feminine（フェミニン）というのは、「女性らしい」という英語のカタカナ語で、女性らしいファッションを身にまとう男性を意味しています。少なくとも男らしくはなかったわけですね。マッチョな今の武田真治とは真逆のイメージです。

そして、かくいう私も、私の姿を見たことがある方がご存じでしょうが、かなり厳ついですし、「ゴツい」といわれる体格をしていますが、小学生の頃は、細身で、ひ弱な体をしていました。私の子どもの頃の写真はさすがにすぐに出てこないのですが、簡単に言えば、身長は高かったもののひょろりとした「もやし」みたいな子供でした。また、運動も得意では無く、サッカーや野球、バスケットボールやバレーボールといった球技はまるでダメでした。

更に私の場合、父が転勤族であったせいもあり、新しい学校に編入するたびに、イジメを受けたものです。体が弱く、運動神経もない私は困りました。そこで、イジメに対抗する方法として、私は体力を養ったり格闘技（空手、剣道、柔道）を学びました。そして、小学生高学年の頃には、極真空手から枝分かれした超実践派空手である大道塾（顔面パンチあり、投げや関節技あり）で空手初段（児童の部での初段）の有段者になり、大会でも準決勝ぐらいまで進出できるようになりました。腹筋もいわゆるシックスパックにバキバキに割れるようになり、もう誰も私を虐めるどころか、同級生の間で「あいつは強すぎる」と一目を置かれるようになりました。

つまり、虚弱であるとか、運動神経に自信が無いという生徒でも、こと筋肉）は裏切りません。そして、それと同じようにや数学（算数）も（算数）も、本人の資質やセンスなどには左右されず、努力をすれば決して裏切ることはないのです。数学（算数）は筋トレと同じく、やればやっただけ、頭の良さとかセンスとか一切関係なく、確実に伸びる科目です。数学（算数）は繰り返しすればするほど、必ず学力が向上する、決して裏切らない科目であるのです。

ちなみに、保護者の皆さんも数学が苦手だという方は、必ずこんな思い出があるはずです。「あー因数分解で訳が分からなくなって、数学が苦手になった」だとか「二次方程式で挫折した」とか、しかし、このとき皆さんは勉強しましたでしょうか？苦手を克服しようと、他の科目以上に努力したでしょうか？大抵はそうではないと思います。「苦手だ」と感じてしまったそのときから、もう数学の勉強を止めてしまったのではないでしょうか。そして、勉強しなければどんどん筋トレをサボって筋肉が落ちていくように、数学力が落ちていきます。当然、数学力が落ちてくれば、ますます数学が嫌いになるという悪循環に陥るわけですね。

02　数学の記号に慣れること

また、数学の記号を毛嫌いされる方も多いと思います。数学には、さまざまな日常生活では見慣れない数学記号が登場します。これがまた、学校の先生が細かく説明をしてくれず、さらっと一回だけ説明して、次は即問題などでその記号を使って問題を解いていくので、記号の意味をきちんと理解し、消化できていないと、その段階で落ちこぼれてしまいます。皆さんも少し昔のことを思い出してみてください。初歩的な例で言うと、これは高校数学の最初に出てきた数学Aの記号「P」であるとか「C」です。

順列《武蔵境駅徒歩30秒》武蔵野個別指導塾組合せ《武蔵境駅徒歩30秒》武蔵野個別指導塾

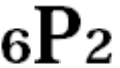
とか書いたりしますよね。この記号を見た瞬間中身の説明を聞こうともせず、フリーズしてしまって、「数学は嫌いだ」と思ってしまった方、意外と少なくないと思います。これは、先ほどお話ししました通り、学校の先生にも問題があると思うのですが、きちんと丁寧に説明してくれないケースが多いですし、こういう記号を使うと一体何が得なのか、何に役立つのか教えてくれなかったりするんですね。すると、いきなり、言葉の説明もおろそかに、数学の授業が始めってしまうと、当然多くの人はやる気を失ってしまうわけです。

しかし、Pとは「permutation(パーミュテーション)」という並び替えという英語の単語の頭文字から来ていますし、「ピー」と読めばいいだけですし、Cも英語の「combination」という組み合わせという意味の英単語の頭文字から来ているだけで、「シー」と読めばいいだけです。こう聞くと、なんだPとかCとかいうけど、意味は簡単じゃないかと思ってくれると思います。さらに、使い方も別に難しくなく、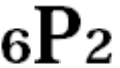順列《武蔵境駅徒歩30秒》武蔵野個別指導塾と書けば、6から2から1つずつ減った数の積（かけ算）をすれば良いだけです。つまり、Pの左側の数字を順に、Pの右側の数字の回数だけ一つずつ減っていく数を繰り返し書けていくというだけですね。式として現せば、

6×5＝30

です。どうでしょうか。これが、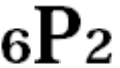順列《武蔵境駅徒歩30秒》武蔵野個別指導塾という記号の表している意味ですね。日本語で言えば、「6を6から1つずつ減らして、6×5と二回書けてくれればいい」と言っているだけなんですね。「なんだ、そんな簡単なことにPとか難しい記号を使うなよ」と思われた方もいるかもしれませんが、いちいち、「5P3と書くのでは無く、5を5から一つずつ減らして、5×4×3と三回掛けてくれ。そして、4P2なら、4を4から一つずつ減らして、4×3と二回掛けてくれ」というと何度も出てくると、確かにうざい説明になりますね。

また、こういう概念を使った問題を解くとき、たとえば「5個の異なる果物から3個を選んで1個ずつ食べるとき、食べる順序は何通りあるのか」と問われたとき、「えーと、最初に5個の中から一つ選ぶわけだから5通りで、次に残った4個の中から1つ選ぶわけだから4通りだ、そして最後に残った3個の中から選ぶわけだから、3通り、つまり、5×4×3＝60で、60通りある」なんて答えると結構面倒くさいですよね。素直にPを受け入れて、「5個の異なる果物の中から3個を一つずつ選んでいくのだから、5P3、つまり、5×4×3＝60だ」と答える方が楽ですし、考えるときも頭がすっきりしないでしょうか。

高校数学、あるいは、数学Aというだけで苦手意識を持ってしまう生徒さんはもちろん、保護者の方も少なくないのですが、言葉の意味と読み方、使い方を教えれば、九九を覚えた小学生低学年でも理解できる概念だと思います。実際、中学受験算数などでは、記号は使いませんが、こういう考え方をします。

同じように組合せ《武蔵境駅徒歩30秒》武蔵野個別指導塾も、これはCの左側を分子に持って行き、Cの右側を分母に持っていた上で、分母と分子の両方にCの右側の数だけかけていけばいいだけという意味です。この例で言えば、（分子）7×6×5/3×2×1を計算すればいいだけです。つまり、この場合は、Cの左側が分子、右側が分母となるわけです。計算すると、（7×6×5）/（3×2×1）となり、210/6、約分して、105/3ですね。これもさっきと同様、小学生でも理解できる話でこれも中学受験数学ではこういう風に小学生も理解して解きます、要するに何が言いたいのかと言いますと、数学はきちんと説明を聞き、参考書を読み、復習していけば、努力に比例して点数が上がっていく一番取り組みやすい科目となります。

03　数学（算数）が得意になるための学習法とは

それでは、数学（算数）が得意になる学習法というのはどのような学習の仕方なのでしょうか。分かりやすく理解できるように、ここにAくんとBくんの二人の勉強を見てみましょう。

Aくんは、こういう学習の仕方をしています。

・1冊のテキスト、問題集をやり通すことができず、すぐに飽きてしまい、次から次へと新しい教材に手を出したらやりっぱなしで、できなかった問題についても特に復習しない。とりあえず、最低限の公式だけを渋々覚えることだけはしています。また、初めて見る問題に当たってしまうと、問題毎に思いつきの解法を編み出すことでなんとか解こうとします。定期試験や実力試験の前だけさっと復習し、同じ問題を解いても意味が無いと思っています。テストや模試の結果も正解か不正解かだけに一喜一憂し、解けなかった問題の解き直しは面倒だと考えています。問題集を解く際には、解けた問題も解けなかった問題も特に分けること無く、間違えたものだけ×をつけて、「あー、こんなに間違えた」といって、解答だけを見て正解の答えだけをノートなり、問題集に直接書き移し、それで問題集を解くのはおしまいにします。

それに対して、Bくんは次のような学習の仕方をしています。

・1冊のテキストや問題集をひたすら繰り返し、できなかった問題は、できるようになるまで何度でも繰り返して解き直しをします。また、「解き方」を覚えるのはもちろん、「考え方」も重視します。模試や定期試験を受けた際には必ず間違えた問題を解き直しし、分からないまま次の単元に進んでしまうことがないようにしています。分からないところは、解説を何度も読んだり、聞いたりして、自分が腑に落ちるまで、しっかり理解しようと取り組みます。問題集を解いた際も自力で解けたものには「○」をつけ、解説を読んで理解したものは「△」、解説を読んでも理解できなかったものは「×」などと自分の頭の中で問題のでき具合を整理しています。そして、こうして整理した問題のうち、×が△に、△が○になるまで、何度も解き直します。

如何でしょうか。AくんとBくんどちらが数学（算数）の成績が上がっていくと思われますでしょうか。これはかなりわかりやすくデフォルメして書いているので、一目瞭然でBくんだ、と思われると思います。しかし、それは私が半ば誘導的にBくんの学習法が良いように書いているので、当然そう思われるだけかもしれません。なので、Bくんの学習法で重要なポイントを下に箇条書きしましょう。

できたかできなかったかだけで判断するのではなく、できるようになるまで繰り返し復習すること
問題の正解不正解に一喜一憂するのではなく、「解き方」や「考え方」を理解しようとすること
解説や説明を自分が腑に落ちるまで理解しようとすること
問題集などに取り組む際にただ○×だけをつけるのではなく、問題への理解度を整理すること
問題集などの問題でできなかった問題を繰り返し解き直すこと

といった具合でしょうか。逆に、Aくんの学習法で問題なのは、中途半端な取り組みによる消化不良が発生しているというところに尽きるでしょう。問題集、参考書、定期試験、模試などで間違えた問題に一喜一憂するだけで、復習をせず、次々と新しい問題に取り組んでいるため、一つ一つの問題をきちんと理解することができていません。理解できなかった問題がある場合、それが理解できるまで取り組まなければ、結局全て中途半端になってしまい、最終的には、その中途半端な積み重ねで、結局何が何だか分からなくなってしまいます。行き当たりばったりで、根本的な理解に至れていないわけですね。

数学（算数）の問題のパターンは、一見無限に見えますが、実際、入試問題で出題されるパターンは有限です。入試では、必ず、同じような問題が出題されます。初めて見るタイプの問題が出ることはかなり珍しく、仮に初めて見るタイプの問題でも、それまでの解法のパターンを知っていればそれを応用して解ける問題になっています。つまり、問題のパターンを知り、その解法を知っておくと、後は数字を入れ替えただけで解けるようになるのが、数学（算数）という科目なわけです。このことをもう少しまとめると、数学（算数）が得意になるためには、